Answer: Option C)
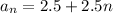
Explanation:
Note that the sequence increases by a factor of 2.5, that is, each term is the sum of the previous term plus 2.5.
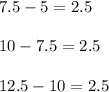
therefore this is an arithmetic sequence with an increase factor d = 2.5
The linear formula for the sequence
 is:
is:
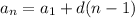
Where
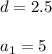
 is the first term of the sequence
is the first term of the sequence
So
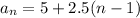
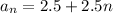
The answer is the option C)