A line passes through the origin and has a slope of -3 what is the equation of the line that is perpendicular to the first line and passes through the point (3,4)?

Question

asked Aug 13, 2020 27.7k views

2 Answers

Vdelricco · Answer 1 · 2020-08-16T10:06:07+0000

ANSWER

y= (1)/(3) x + 3

EXPLANATION

We want to find the equation of a line which is perpendicular to another line with slope -3 and passes through (3,4).

Our line of interest is has a slope that is the negative reciprocal of -3

m = - (1)/( - 3) = (1)/(3)

The equation is given by

y-y_1=m(x-x_1)

We substitute the point and slope to get:

y-4= (1)/(3) (x-3)

Expand

y-4= (1)/(3) x-1

y= (1)/(3) x-1 + 4

y= (1)/(3) x + 3

Sudhir · Answer 2 · 2020-08-19T14:11:37+0000

Answer:
y=(1)/(3)x+3

Explanation:

The equation of the line is Slope-intercept form is:

y=mx+b

Where "m" is the slope and "b" the y-intercept.

The slopes of perpendicular lines are negative reciprocal.

Then, if the slope of the first line is -3, the slope of the other line must be:

m=(1)/(3)

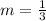
Substitute the point (3,4) into the equation and solve for b:

$4=(1)/(3)(3)+b\\ 4-1=b\\b=3$

Then the equation of this line is:

y=(1)/(3)x+3