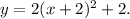2 Answers

Leandro Fournier · Answer 1 · 2020-11-22T23:19:30+0000

Answer:

y=2(x+2) ^ 2 + 2.

Explanation:

For a quadratic equation written in the general form
y=ax ^ 2 + bx + c ,

the x coordinate of its vertex is:

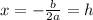
x = -(b)/(2a) = h

Then this equation written in the form of vertex is:

y=a(x-h) ^ 2 + k.

Where the point (h, k) is the vertex of the parabola.

In this case we have the equation

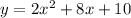
y=2x^2+8x+10

Then the x coordinate of its vertex is:

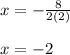
$x=-(8)/(2(2))\\\\x= -2$

Therefore the y coordinate of its vertex is:

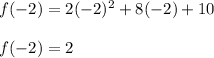
$f(-2) = 2(-2)^2+8(-2)+10\\\\f(-2) = 2$

The vertice is (-2, 2)

Then

$h=-2\\\\k = 2$ .

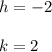This equation written in the form of vertex is

y=2(x+2) ^ 2 + 2.

Please log in or register to add a comment.