Answer:
smallest value of x = -1
Largest value of x = 7
Explanation:
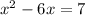
coefficient of x = -6
Half of the coefficient of x = -6/2 = -3
Square of the half value
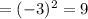
Add the square value on both sides of equation
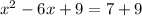
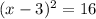
Take square root
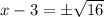
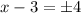
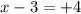 or
or
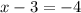
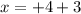 or
or
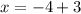
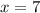 or
or
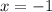
Hence smallest value of x = -1
Largest value of x = 7