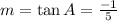Question

Write the equation x+5y-2= 0 in normal form. Then, find the length of the normal and the length and the angle makes with the positive x-axis.

Answer 1

normal form: y = -x/5 + 2/5

Answer 2

Answer with explanation:

≡The given equation of line is :

x + 5 y -2=0------------(1)

⇒A line having equation, Ax +By +C=0, can be written in normal form as Follows:

`\rightarrow (Ax)/(√(A^2+B^2))+ (By)/(√(A^2+B^2))+ (C)/(√(A^2+B^2))=0`

⇒Length of Normal

`=|(C)/(√(A^2+B^2))|`

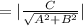
Let, A=Angle made by line with positive Direction of X axis.

`\sin A=(A)/(√(A^2+B^2))\\\\ \cos A=(B)/(√(A^2+B^2))`

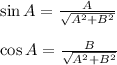
⇒Line, 1 in normal form can be written as:

`x + 5 y=2\\\\\rightarrow(x)/(√(1^2+5^2))+(5 y)/(√(1^2+5^2))=(2)/(√(1^2+5^2))\\\\\rightarrow(x)/(√(26))+(5 y)/(√(26))=(2)/(√(26))`

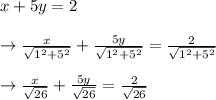
⇒Length of Normal

`=(2)/(√(26))\\\\=0.40\text{approx}`

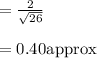
⇒Writing equation of line in slope intercept form

`5 y= -x +2\\\\y=(-x)/(5)+(2)/(5)`

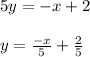
⇒Comparing with general slope intercept form of line:

y = m x +c,

or, y = x tan A +c

`m=\tan A=(-1)/(5)`