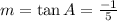Answer with explanation:
≡The given equation of line is :
x + 5 y -2=0------------(1)
⇒A line having equation, Ax +By +C=0, can be written in normal form as Follows:
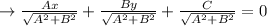
⇒Length of Normal
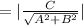
Let, A=Angle made by line with positive Direction of X axis.
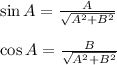
⇒Line, 1 in normal form can be written as:
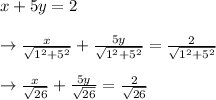
⇒Length of Normal
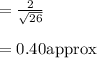
⇒Writing equation of line in slope intercept form
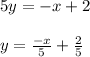
⇒Comparing with general slope intercept form of line:
y = m x +c,
or, y = x tan A +c