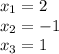For this case we must follow the steps below:
We factor the polynomial, starting by factoring the maximum common denominator of each group:
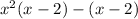
We factor the maximum common denominator
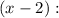
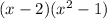
Now, by definition of perfect squares we have:
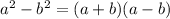
Where:
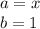
Now, we can rewrite the polynomial as:

To find the roots we equate to 0:
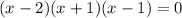
So, the roots are:
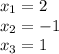
Answer: