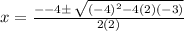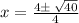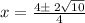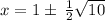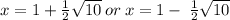ANSWER
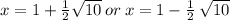
Step-by-step explanation
The given quadratic equation is
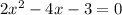
This function is of the form:
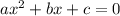
This implies that:
a=2, b=-4 and c=-3.
We can solve this equation using the quadratic formula:
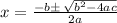
We substitute the values into the quadratic formula to obtain;