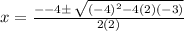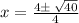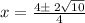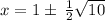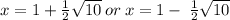Question

How would you solve 2x^2 -4x -3 = 0

Answer 1

`x =1 +(1)/(2) √( 10) \: or \: x =1 - (1)/(2)\: √(10)`

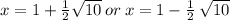
Step-by-step explanation

The given quadratic equation is

`2 {x}^(2) - 4x - 3 = 0`

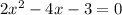
This function is of the form:

`a{x}^(2) + bx + c = 0`

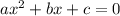
This implies that:

a=2, b=-4 and c=-3.

We can solve this equation using the quadratic formula:

`x = \frac{ - b \pm \: \sqrt{ {b}^(2) - 4ac} }{2a}`

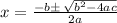
We substitute the values into the quadratic formula to obtain;

`x = \frac{ - - 4 \pm \: \sqrt{ {( - 4)}^(2) - 4(2)( - 3)} }{2(2)}`

`x = (4 \pm \: √( 40) )/(4)`

`x = (4 \pm \: 2√( 10) )/(4)`

`x =1\pm \: (1)/(2) √(10)`

`x =1 +(1)/(2) √( 10) \: or \: x =1 - \: (1)/(2) √(10)`