Answer:
The last graph
Explanation:
The problem presented here is similar to a compound interest problem since we have an initial value, a growth constant and the aspect of time.
We can consider the number of television sets currently produced by the company to be our Principal amount;
P = 2000
The rate of increase in production per month can be considered as our interest rate earned;
r = 25% = 0.25
The total number of television sets y will be our Accumulated amount;
A = y
The duration x becomes our time n.
The compound interest formula is given as;
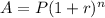
We simply substitute the given information into the formula;
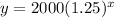
This is an exponential growth function since the base of the exponent x is greater than 1.
A graph of the function will be an exponential curve passing through ( 0, 2000) since 2000 is our initial value