Rewrite The following expression.

Question

asked Jun 12, 2020 140k views

2 Answers

Cocotton · Answer 1 · 2020-06-14T03:59:50+0000

Answer:

Choice A is correct

Explanation:

We have been given the expression;

$x^{(9)/(7) }$

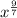
In order to re-write this expression, we shall use some laws of exponents;

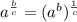
$a^{(b)/(c) }=(a^(b))^{(1)/(c) }$

Using this law, the expression can be written as;

$(x^(9))^{(1)/(7)}$

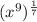
The next thing we need to remember is that;

$a^{(1)/(n) }=\sqrt[n]{a}$

Therefore, the expression becomes;

$\sqrt[7]{x^(9) }$

Next,

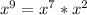
x^(9)=x^(7)*x^(2)

This implies that;

$\sqrt[7]{x^(9) }=\sqrt[7]{x^(7)*x^(2)}\\=\sqrt[7]{x^(7) }*\sqrt[7]{x^(2) } \\=x\sqrt[7]{x^(2) }$

TheRealFakeNews · Answer 2 · 2020-06-18T09:48:04+0000

ANSWER

A.

$x \sqrt[7]{{x}^(2) } .$

EXPLANATION

The given expression is

${x}^{ (9)/(7) }$

We want to rewrite the given expression in radical form:

Recall that:

${a}^{ (m)/(n) } = \sqrt[n]{ {a}^(m) }$

This implies that:

${x}^{ (9)/(7) } = \sqrt[7]{ {x}^(9) }$

${x}^{ (9)/(7) } = \sqrt[7]{ {x}^(7) * {x}^(2) }$

Split the radicals.

${x}^{ (9)/(7) } = \sqrt[7]{ {x}^(7) } * \sqrt[7]{{x}^(2) }$

This finally simplifies to:

${x}^{ (9)/(7) }=x \sqrt[7]{{x}^(2) }$

The correct answer is A.