Answer:

Explanation:
Given the function f(x):
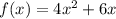
And the function g(x):
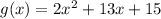
To find
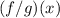 you need to divide the function f(x) by the function g(x).
you need to divide the function f(x) by the function g(x).
Therefore, knowing this, you get:

You can simplify the numerator by factoring out 2x:
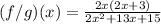
You have to simplify the denominator:
Rewrite the term 13x as a sum of two terms whose product be 30:

Apply Distributive property:
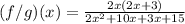
Make two groups of two terms:

Factor out 2x from the first group and 3 from the second group:

Factor out (x+5):
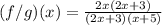
Simplifying, you get:
