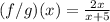Question

Given
`f(x)= 4x^2 + 6x and g(x) = 2x^2 +13x+15 \\`, find (f/x) (x)

Answer 1

`( (f)/(g) )(x) = (2x )/(x + 5)`

where

`x \\e - (3)/(2) \: or \: x = - 5`

EXPLANATION

The given functions are:

`f(x) = 4 {x}^(2) + 6x`

and

`g(x) =2 {x}^(2) + 13x + 15`

We want to find ,

`( (f)/(g) )(x) = (f(x))/(g(x))`

`( (f)/(g) )(x) = \frac{4 {x}^(2) + 6x }{2 {x}^(2) + 13x + 15}`

`( (f)/(g) )(x) = \frac{2x(2x + 3) }{2{x}^(2) + 10x +3x + 15}`

`( (f)/(g) )(x) = \frac{2x(2x + 3) }{2{x}(x + 5) +3(x + 5)}`

`( (f)/(g) )(x) = (2x(2x + 3) )/((2x + 3)(x + 5))`

We cancel out the common factors to get:

`( (f)/(g) )(x) = (2x )/(x + 5)`

where

`x \\e - (3)/(2) \: or \: x = - 5`

Answer 2

Answer:
`(f/g)(x)=(2x)/(x+5)`

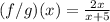
Explanation:

Given the function f(x):

`f(x)=4x^2+6x`

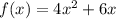
And the function g(x):

`g(x)=2x^2+13x+15`

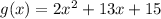
To find
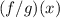`(f/g)(x)` you need to divide the function f(x) by the function g(x).

Therefore, knowing this, you get:

`(f/g)(x)=(4x^2+6x)/(2x^2+13x+15)`

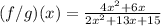
You can simplify the numerator by factoring out 2x:

`(f/g)(x)=(2x(2x+3))/(2x^2+13x+15)`

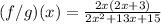
You have to simplify the denominator:

Rewrite the term 13x as a sum of two terms whose product be 30:

`(f/g)(x)=(2x(2x+3))/(2x^2+(10+ 3)x+15)`

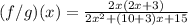
Apply Distributive property:

`(f/g)(x)=(2x(2x+3))/(2x^2+10x+ 3x+15)`

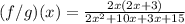
Make two groups of two terms:

`(f/g)(x)=(2x(2x+3))/((2x^2+10x)+ (3x+15))`

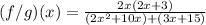
Factor out 2x from the first group and 3 from the second group:

`(f/g)(x)=(2x(2x+3))/((2x(x+5))+ 3(x+5))`

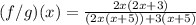
Factor out (x+5):

`(f/g)(x)=(2x(2x+3))/((2x+3)(x+5))`

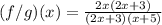
Simplifying, you get:

`(f/g)(x)=(2x)/(x+5)`