Hello!
The answer is:
The equation is:
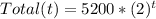
Why?
It's an exponential growth problem, we can calculate the exponential growth using the following equation:

Where,
Total, is the total population after "t" time in days.
Start population, for this is equal to 5,200
r,is equal to the percent of growth, for this case it's 100% each day.
t, is the time elapsed.
So, rewriting the equation, we have:
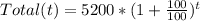
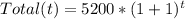
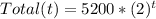
Have a nice day!