Answer:
The radius is
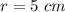
Explanation:
we know that
The inscribed angle is half that of the arc it comprises.
so
![m<C =(1/2)[arc\ AB]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/zznj4medb2t9hmw1tolgsjii3o28qum1z4.png)

substitute
![90\°=(1/2)[arc\ AB]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4xyvfgp9jwumssouaowgffxf0flo8ebak7.png)
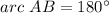
That means----> The length side AB of the inscribed triangle is a diameter of the circle
Applying Pythagoras Theorem
Calculate the length side AB
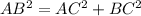
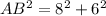
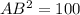
 -----> is the diameter
-----> is the diameter
Find the radius
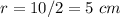 -----> the radius is half the diameter
-----> the radius is half the diameter