Question

A right triangle △ABC with right angle C is inscribed in a circle. Find the radius of this circle if: Given m∠C = 90°, k(O, r) inscribed in △ABC, AC = 8 cm, BC = 6 cm. Find r.

Answer 1

The radius is
`r=5\ cm`

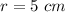
Explanation:

we know that

The inscribed angle is half that of the arc it comprises.

so

`m<C =(1/2)[arc\ AB]`

`m<C =90\°`

substitute

`90\°=(1/2)[arc\ AB]`

`arc\ AB=180\°`

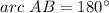
That means----> The length side AB of the inscribed triangle is a diameter of the circle

Applying Pythagoras Theorem

Calculate the length side AB

`AB^(2)=AC^(2)+BC^(2)`

`AB^(2)=8^(2)+6^(2)`

`AB^(2)=100`

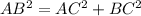
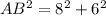
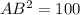
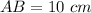`AB=10\ cm` -----> is the diameter

Find the radius

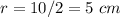`r=10/2=5\ cm` -----> the radius is half the diameter