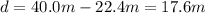(a) 35.0 N/m
The period of a simple harmonic motion is given by:
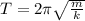
where
m is the mass attached to the spring
k is the spring constant
In this problem, we have:
T = 9.5 s is the period of the motion
m = 80.0 kg is the mass of the bungee jumper attached to the spring
Solving the equation for k, we find the effective spring constant of the cord:
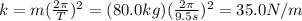
(b) 17.6 m
When the jumper comes to rest, the cord is stretched with respect to its equilibrium position by a certain amount x. In this situation, the force responsible for the stretching of the cord is the weight of the bungee jumper:

Using Hooke's law:
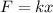
and re-arranging for x, we find the stretching of the cord:
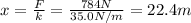
And since the jumper comes to rest at a distance of 40.0 m below the jump point, this means that the unstretched length of the cord is