Answer: second option
Explanation:
The equation of the line in slope-intercept form is:

Where m is the slope and b is the y-intercept.
Rewrite the expression as:
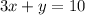
Solve for "y":
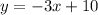
You can identify that:
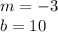
Therefore, the line intersects the y-axis at the point (0,10)
For the graphs of inequalities with
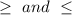 the line must be solid.
the line must be solid.
The inequality given is
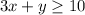 and it can be written as
and it can be written as
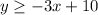
Then, the shaded region must be above the solid line. Therefore it does not include the origin (Observe the graph attached).