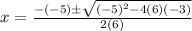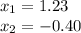Answer:
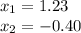
Explanation:
Given a quadratic equation in the form
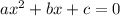 , you can use the Quadratic formula to solve it. This is:
, you can use the Quadratic formula to solve it. This is:
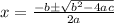
Then, you need to subtract
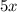 from both sides of the equation given:
from both sides of the equation given:
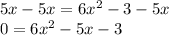
You can identify that:
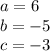
Then, substituting values into the Quadratic formula, you get: