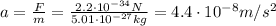Question

Optical tweezers use light from a laser to move single atoms and molecules around. Suppose the intensity of light from the tweezers is 1000 W/m2, the same as the intensity of sunlight at the surface of the Earth. (a) What is the pressure on an atom if light from the tweezers is totally absorbed? ? Pa (b) If this pressure were exerted on a tritium atom, what would be its acceleration? (The mass of a tritium atom is 5.01 ✕ 10−27 kg. Assume the cross-sectional area of the laser beam is 6.65 ✕ 10−29 m2.)

Answer 1

(a)
`3.3\cdot 10^(-6) Pa`

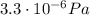
The radiation pressure exerted by an electromagnetic wave on a surface that totally absorbs the radiation is given by

`p=(I)/(c)`

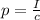
where

I is the intensity of the wave

c is the speed of light

In this problem,

`I=1000 W/m^2`

and substituting
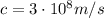`c=3\cdot 10^8 m/s`, we find the radiation pressure

`p=(1000 W/m^2)/(3\cdot 10^8 m/s)=3.3\cdot 10^(-6)Pa`

(b)
`4.4\cdot 10^(-8) m/s^2`

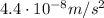
Since we know the cross-sectional area of the laser beam:

`A=6.65\cdot 10^(-29)m^2`

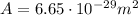
starting from the radiation pressure found at point (a), we can calculate the force exerted on a tritium atom:

`F=pa=(3.3\cdot 10^(-6)Pa)(6.65\cdot 10^(-29) m^2)=2.2\cdot 10^(-34)N`

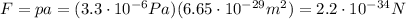
And then, since we know the mass of the atom

`m=5.01\cdot 10^(-27)kg`

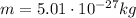
we can find the acceleration, by using Newton's second law:

`a=(F)/(m)=(2.2\cdot 10^(-34) N)/(5.01\cdot 10^(-27) kg)=4.4\cdot 10^(-8) m/s^2`