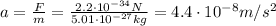(a)
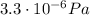
The radiation pressure exerted by an electromagnetic wave on a surface that totally absorbs the radiation is given by
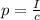
where
I is the intensity of the wave
c is the speed of light
In this problem,
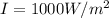
and substituting
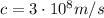 , we find the radiation pressure
, we find the radiation pressure
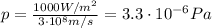
(b)
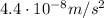
Since we know the cross-sectional area of the laser beam:
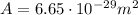
starting from the radiation pressure found at point (a), we can calculate the force exerted on a tritium atom:
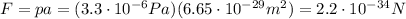
And then, since we know the mass of the atom
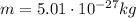
we can find the acceleration, by using Newton's second law: