Answer:
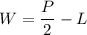
Explanation:
To solve for W, we have to isolate the W-variable. First, we can factor the expression 2L + 2W to 2(L+W):
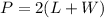
Next, we'll be dividing both sides by 2:
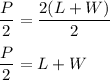
Then subtract both sides by L:
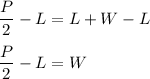
Therefore, we'll obtain W = P/2 - L.
Note that the given formula is perimeter formula of a rectangle where Perimeter = 2 * Length + 2 * Width.
So if we solve for W (Width) then we'll get Width = Perimeter / 2 - Length which can be useful to find width with given perimeter and length.