Answer:
D. around 32 N.
Given that:
- The mass of the moon is approximately
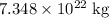 , and
, and - The (mean) radius of the moon is approximately
 .
.
Step-by-step explanation:
The dog is much smaller and lighter than the moon; it behaves like a point mass. Consider the equation for the size of gravity between a spherical mass and a point mass outside that spherical mass:
 ,
,
where
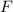 is the size of gravity,
is the size of gravity,- The gravitational constant
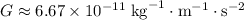 ,
,
 is the mass of the sphere,
is the mass of the sphere,
 is the size of the point mass, and
is the size of the point mass, and
 is the separation between the point mass and the center of mass of the sphere.
is the separation between the point mass and the center of mass of the sphere.
The dog is at the surface of the moon. As a result, the
 shall be the same as the radius of the moon. Make sure all values are in SI units (kilograms and meters.) Apply the formula:
shall be the same as the radius of the moon. Make sure all values are in SI units (kilograms and meters.) Apply the formula:
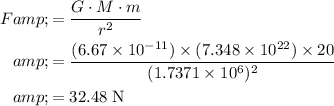 .
.
This value may vary slightly depending on the position of the dog on the moon.