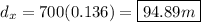Question

A horizontal rifle is fired at a bull's-eye. The muzzle speed of the bullet is 700 m/s. The barrel is pointed directly at the center of the bull's-eye, but the bullet strikes the target 0.09 m below the center. What is the horizontal distance between the end of the rifle and the bull's-eye?

Answer 1

First, we need to know how much time it takes to hit the bull's eye :

h = 1/2 • g • t²

(0.09 m) = ½ (9.81 m/s²) t²

t = 0.135 s

Then, we will know the distance between the rifle and the bull's eye :

X = v • t

X = (700 m/s)(0.135 s)

X = 94.5 m

Answer 2

Hi there!

We can begin by solving for the time taken for the bullet to travel a VERTICAL distance of 0.09 m due to the effects of gravity.

We can use the kinematic equation for uniform acceleration:

`d_y = v_(0y)t + (1)/(2)at^2`

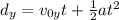
Since there is no initial vertical velocity:

`d_y = (1)/(2)at^2`

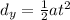
Rearrange to solve for time. (a = g = 9.8 m/s²)

`t = \sqrt{(2d)/(g)}`

`t = \sqrt{(2(0.09))/(9.8)} = 0.136 s`

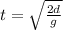
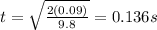
Now, we can use the distance, speed, and time equation in the horizontal direction:

`d_x = v_xt`

Plug in the values:

`d_x = 700(0.136) = \boxed{94.89 m}`