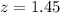For this case we have the following equation:
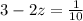
We must find the value of z that represents the solution of the equation:
We follow the steps below:
We multiply by 10 on both sides of the equation:
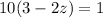
We apply distributive property to the terms of parentheses;
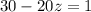
We subtract 30 from both sides of the equation:
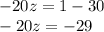
We divide between -20 on both sides of the equation:
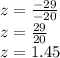
If we substitute the value of z in the original equation, equality is satisfied.
Answer: