Question

Find the exact value of the following expression (without using a calculator): tan(Sin^-1 x/2)

Answer 1

tan(Sin^-1 x/2)=
`\frac{x/2}{\sqrt{1-x^(2)/4 } }`

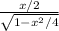
Explanation:

Let sin^-1 x/2= θ

then sinθ= x/2

on the basis of unit circle, we have a triangle with hypotenuse of length 1, one side of length x/2 and opposite angle of θ.

tan(Sin^-1 x/2) = tanθ

tanθ= sinθ/cosθ

as per trigonometric identities cosθ= √(1-sin^2θ)

tanθ= sinθ/ √(1-sin^2θ)

substituting the value sinθ=x/2 in the above equation

tanθ=
`\frac{x/2}{\sqrt{1-x^(2)/4 } }`

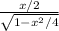
now substituting the value sin^-1 x/2= θ in above equation

tan(sin^-1 x/2) =
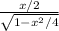
`\frac{x/2}{\sqrt{1-x^(2)/4 } }`

!