Answer:
tan(Sin^-1 x/2)=
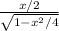
Explanation:
Let sin^-1 x/2= θ
then sinθ= x/2
on the basis of unit circle, we have a triangle with hypotenuse of length 1, one side of length x/2 and opposite angle of θ.
tan(Sin^-1 x/2) = tanθ
tanθ= sinθ/cosθ
as per trigonometric identities cosθ= √(1-sin^2θ)
tanθ= sinθ/ √(1-sin^2θ)
substituting the value sinθ=x/2 in the above equation
tanθ=
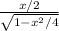
now substituting the value sin^-1 x/2= θ in above equation
tan(sin^-1 x/2) =
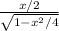
!