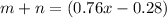Answer:
Part 1) The maximum number of pounds of regular coffee that you can buy is 7.5 pounds.
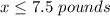
Part 2)
Explanation:
Part 1)
Let
x-----> the number of pounds of regular coffee
we know that
The inequality that represent the situation is

Solve for x
Divide by 2 both sides
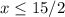
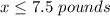
The maximum number of pounds of regular coffee that you can buy is 7.5 pounds.
The solution of the inequality is the interval ------> (-∞,7.5]
but the number of pounds cannot be a negative number
therefore
The solution is the interval -----> [0,7.5]
see the attached figure
Part 2) we have
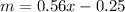
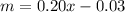
Adds m and n
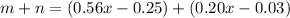
Group terms that contain the same variable
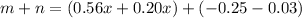
Combine like terms