Question

a train is moving at a constant speed on a surface and inclined at 10 degrees with the horizontal travels a distance of 400 m in 5 Seconds. calculate the vertical velocity component of the train during the time period.

Answer 1

13.9 m/s

Step-by-step explanation:

The velocity of the train along the inclined surface is given by the ratio between the distance travelled, d, and the time taken, t:

`v=(d)/(t)`

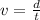
where we have

d = 400 m

t = 5 s

Substituting,

`v=(400 m)/(5 s)=80 m/s`

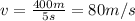
This is the velocity of the train along the inclined plane. Now we can find the vertical component of the velocity by using the formula:

`v_y = v sin \theta`

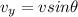
where
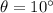`\theta=10^(\circ)` is the angle of the slope. Substituting, we find

`v_y = (80 m/s)(sin 10^(\circ))=13.9 m/s`