Answer:
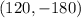
Explanation:
The given parametric equation is
x=2t
y= -3t
The coordinates of any point lying on this curve can be obtained by substituting the parameter value.
Given the parameter value, t=60
We have
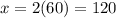
and
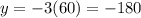
Therefore the point
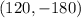
lie on this parametric curve.