Answer:
B) (21, -14) and (21, -22)
Explanation:
Given,
The area of the square = 64 square unit,
Let x be the side of the square,
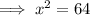
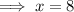
Hence, the side of the square = 8 unit,
⇒ The distance between the adjacent vertices in the square = 8 units,
By the distance formula,
The distance between (3, -35) and (3, -28) is,
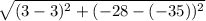

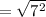
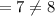
Thus, (3, -35) and (3, -28) can not be the vertices of the square.
The distance between (21, -14) and (21, -22) is,
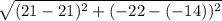
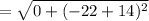
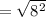
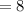
Thus, (21, -14) and (21, -22) are the vertices of the square.
The distance between (32, -42) and (32, -7) is,

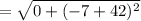
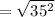

Thus, (32, -42) and (32, -7) can not be the vertices of the square.
The distance between (74, 19) and (82, 27) is,
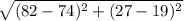
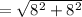
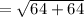
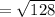
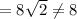
Thus, (74, 19) and (82, 27) can not be the vertices of the square.