Question

A person invest $1200 in an account that earns 2% interest compound quarterly. Find when the value of the investment reaches $1500.00

Formula

A=P(1+r/m)mt

Answer 1

After 11 years the value of the investment reaches $1500.00

.

Explanation:

The formula used for finding time (when the value reaches certain amount) is:

`A= P(1+(r)/(n))^(nt)`

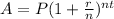
where A= Future VAlue

P= Principal Value

r= rate of interest (in decimal)

n= no of times investment is compounded

t= time

Putting the values given and finding Time t,

A= $1500

P= $1200

r= 2% or 0.02

n= 4 (compound quarterly)

`A= P(1+(r)/(n))^(nt)`

`1500= 1200(1+(0.02)/(4))^(4t)`

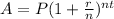
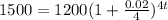
Dividing both sides by 1200 and solving 0.02/4 = 0.005

`1.25= (1+0.005)^(4t)`

`1.25= (1.005)^(4t)`

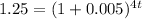
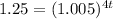
Since t is in power we take the logarithm ln on both sides.

The rule of logarithm says that the exponent can be multiplied with the base when taking log

`\ln1.25=ln( 1.005)^(4t)\\\ln1.25=4t * ln( 1.005)\\0.22 = 4t * 0.005\\Solving\,\,\\(0.22)/(4*0.005) = t\\=> t= 11\, years`