Answer: The correct option is
(c)
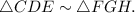
Step-by-step explanation: We are given to write a similarity statement for the triangles shown in the figure.
In the given triangles, we have
m∠C = 60°, m∠D = 53°, m∠F = 60° and m∠H = 67°.
Fist, we have to fin d the measures of angles E and G.
From angle sum property of a triangles, we can write
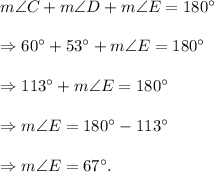
Similarly, we have
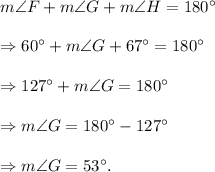
So, we get
m∠C = m∠F,
m∠D = m∠G
and
m∠E = m∠H.
Therefore, by angle-angle-angle similarity postulate. we get
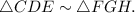
Thus, option (c) is CORRECT.