Question

Write a similarity statement for the triangles.

Answer 1

`\large\boxed{c.\ \triangle CDE\sim\triangle FGH}`

Explanation:

`\text{Calculate the maeasure of the angle}\ E:\\\\180^o-(60^o+53^o)=180^o-113^o=67^o\\\\\angle C\cong\angle F\\\\\angle E\cong\angle H\\\\\angle D\cong\angle G\\\\\text{Therefore:}\\\\\triangle CDE\sim\triangle FGH`

Answer 2

Answer: The correct option is

(c)
`\triangle CDE\sim \triangle FGH.`

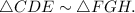
Step-by-step explanation: We are given to write a similarity statement for the triangles shown in the figure.

In the given triangles, we have

m∠C = 60°, m∠D = 53°, m∠F = 60° and m∠H = 67°.

Fist, we have to fin d the measures of angles E and G.

From angle sum property of a triangles, we can write

`m\angle C+m\angle D+m\angle E=180^\circ\\\\\Rightarrow 60^\circ+53^\circ+m\angle E=180^\circ\\\\\Rightarrow 113^\circ+m\angle E=180^\circ\\\\\Rightarrow m\angle E=180^\circ-113^\circ\\\\\Rightarrow m\angle E=67^\circ.`

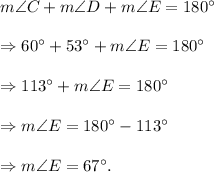
Similarly, we have

`m\angle F+m\angle G+m\angle H=180^\circ\\\\\Rightarrow 60^\circ+m\angle G+67^\circ=180^\circ\\\\\Rightarrow 127^\circ+m\angle G=180^\circ\\\\\Rightarrow m\angle G=180^\circ-127^\circ\\\\\Rightarrow m\angle G=53^\circ.`

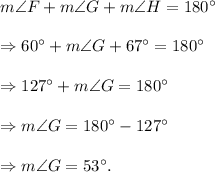
So, we get

m∠C = m∠F,

m∠D = m∠G

and

m∠E = m∠H.

Therefore, by angle-angle-angle similarity postulate. we get

`\triangle CDE\sim \triangle FGH.`

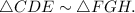
Thus, option (c) is CORRECT.