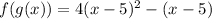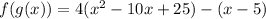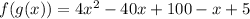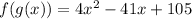Answer: Option B
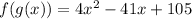
Explanation:
We have 2 functions
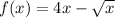
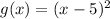
We must find
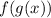
To find this composite function enter the function g(x) within the function f(x) as follows
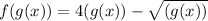
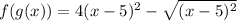
By definition
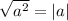
So
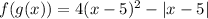
Since x is greater than 5 then the expression
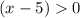 .
.
Therefore we can eliminate the absolute value bars