Answer:
15.4% (nearest tenth)
Explanation:
Estimated volume of the shipping box = 1050 in³
Actual volume of the shipping box using the given dimensions:
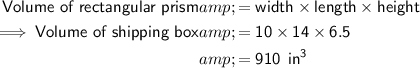
Percent Error formula
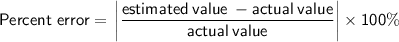
Substitute the estimated and actual volumes into the formula and solve for percent error:
