Question

Solve 3^x+1 = 15 for x using the change of base formula log base b of y equals log y over log b

Answer 1

The value of x is 1.46.

Explanation:

Given : Equation
`3^(x+1)=15`

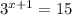
To find : Solve for x using the change of base formula log base b of y equals log y over log b ?

Solution :

Equation
`3^(x+1)=15`

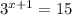
Applying the logarithmic property,

`a^x=b\Rightarrow \log_a(b)=x`

`3^(x+1)=15\Rightarrow \log_3(15)=x+1`

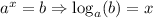
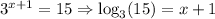
Applying change base formula in LHS,

`log_b(y)= (log y)/(log b)`

`(log 15)/(log 3)=x+1`

`2.46=x+1`

`x=2.46-1`

`x=1.46`

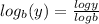
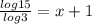
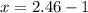
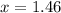
Therefore, the value of x is 1.46.

Answer 2

x= 1.46497

Explanation:

`3^(x+1) = 15`

To solve this , first we convert the exponential form in to log form

`if \ a^x=b \ then \ log_a(b)=x`

`3^(x+1) = 15` becomes
`log_3(15)= x+1`

now we apply change of base formula to remove base 3

`log_b(y)= (log y)/(log b)`

like that log_3(15) becomes

`log_3(15)= (log 15)/(log 3)`

`(log 15)/(log 3)= x+1`

2.46497=x+1

subtract 1 from both sides

x= 1.46497