Question

The width of a box is 1 cm less than its length. The height of the box is 9 cm greater than the length. The dimensions can be represented by x, x − 1, and x + 9. Multiply the dimensions and find the greatest common factor of the terms.

A. x^4
B. x^3
C. x^2
D. x

Answer 1

Option D) x

Explanation:

Let x be the length of the box. Then, we are given that:

Width of box =
`x-1`

Height of box =
`x + 9`

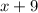
The volume of box is obtained by multiplying these terms.

`x* (x-1)* (x+9)\\=(x^2 - x)* (x+9)\\=(x^2* x) + (x^2* 9) -(x* x)- (x* 9)\\=x^3 + 9x^2 - x^2 - 9x\\= x^3 + 8x^2 - 9x`

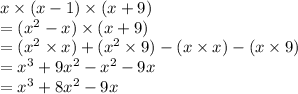
Now, in order to find greatest common factor:

`x^3 + 8x^2 - 9x\\=x(x^2 + 8x - 9)`

Hence, x is the greatest common factor of the terms of the expression as x could be taken as common from each term of the expression obtained.

Answer 2

D. x

Explanation:

The dimensions are:

`x(x-1)(x+9)`

We multiply out the dimensions to obtain;

`x(x^2+9x-x-9)`

`x(x^2+8x-9)`

`x^3+8x^2-9x`

The terms are:

`x^3`

`8x^2=2^3x^2`

`-9x=-3^2x`

The highest common factor is the product of the least powers of th comon factors.

TheHCF is x