Answer:
Option D) x
Explanation:
Let x be the length of the box. Then, we are given that:
Width of box =
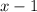
Height of box =
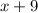
The volume of box is obtained by multiplying these terms.
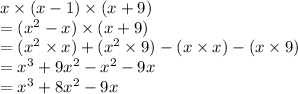
Now, in order to find greatest common factor:
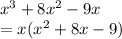
Hence, x is the greatest common factor of the terms of the expression as x could be taken as common from each term of the expression obtained.