Answer:
y = -2x + 3
Explanation:
The given equation is:
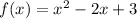
First we need to find the slope of the tangent line. This can be done by finding the derivative of the given function.
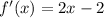
Slope of the tangent will be the value of the derivative at the given point. So the slope of tangent is:

Now we have slope of the tangent line and a point (0, 3) on the tangent. The point (0,3) is the y-intercept of the tangent line. So we can use slope-intercept form to directly write the equation of the line.
The slope intercept form of an equation is:
y = mx + c
where m is the slope and c is the y-intercept.
Using the values: m = -2 and c = 3, we get:
y = -2x + 3
This equation represents the tangent line