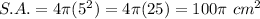1 Answer

Yervand Khalapyan · Answer 1 · 2020-02-23T04:34:26+0000

Answer:

C. 100π

Explanation:

The formula of a volume of a sphere:

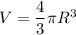
$V=(4)/(3)\pi R^3$

The formula of a surface area of a sphere:

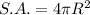
$S.A.=4\pi R^2$

R - radius

We need the length of the radius to calculate the area of the sphere.

Calculate it from the volume of the sphere.

We have a volume:

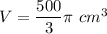
$V=(500)/(3)\pi\ cm^3$

Substitute to the formula of a volume:

$(4)/(3)\pi R^3=(500)/(3)\pi R^3$ divide both sides by π

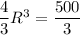(4)/(3)R^3=(500)/(3) multiply both sides by 3

4R^3=500 divide both sides by 4

$R^3=125\to R=\sqrt[6]{125}\\\\R=5\ cm$

Put the value of radius to the formula of a surface area of a sphere:

$S.A.=4\pi(5^2)=4\pi(25)=100\pi\ cm^2$