Which function , A or B has a greater rate of change ? Be sure to include the values for the rates of change in your answer . Explain your answer in words please .

Question

asked Nov 17, 2020 73.4k views

1 Answer

Ruble · Answer 1 · 2020-11-21T19:53:28+0000

A rate of change tells us how one quantity changes in relation to another quantity. In a mathematical language, we can write this as follows:

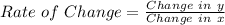
$Rate \ of \ Change=(Change \ in \ y)/(Change \ in \ x)$

For linear functions. the rate of change is the slope of the line. Thus:

FOR THE TABLE:

By taking two points we can get the rate of change, so let's take
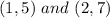$(1,5) \ and \ (2,7)$ :

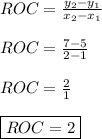
$ROC=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \\ ROC=(7-5)/(2-1) \\ \\ ROC=(2)/(1) \\ \\ \boxed{ROC=2}$

FOR THE GRAPH:

Let's take
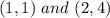$(1,1) \ and \ (2,4)$ :

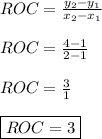
$ROC=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \\ ROC=(4-1)/(2-1) \\ \\ ROC=(3)/(1) \\ \\ \boxed{ROC=3}$

As you can see,
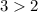3>2 so the ROC of the function given by the graph is greater than the ROC of the function given by the table.