Question

A garage is scheduled to have a temporary gravel floor until the homeowner has the funds necessary to pour a concrete floor. Washed gravel is 105 pounds per cubic foot. If the inside dimensions of the garage are as shown in Exam figure A6, L 35’, W 22’. 18” deep, how much gravel will be required for the floor? Round your answer to the next whole ton. A. 61 tons, B. 138 tons, C. 728 tons, D. 84 tons.

Answer 1

Hello!

The answer is:

A. There will be required 61 tons for the floor.

Why?

To solve the problem, we need to remember how to convert from tons to pounds, and inches to feet.

`1ShortTon=1ton=2000lb`

`1inch=0.083ft`

We are given the density of the whased gravel that is equal to:

`density=(105lb)/(ft^(3) )=(1ton)/(2000lb)=(0.053tons)/(ft^(3) )`

Then, we need to calcualte the volume of the garage in order to know how much gravel will be required for the floor.

First, we need to convert the deep in inches to feet, so:

`18inches*(0.083ft)/(1inches)=1.49=1.5ft`

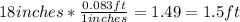
Now, calculating the volume of the garage, we have:

`Volume=length*width*height`

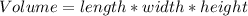
Where, for this case:

`l=35ft\\w=22ft\\\\h=1.5ft`

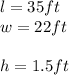
So,

`Volume=35ft*22ft*1.44ft=1155ft^(3)`

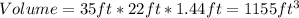
Then, calculating how much gravel will be required for the floor, we have:

`Gravel=Volume*Density=1155ft^(3)*(0.053tons)/(ft^(3))=61.215tons=61tons`

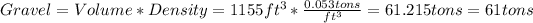
Hence, The answer is A. There will be required 61 tons for the floor.

Have a nice day!