Question

The store salsa jars have a height of ten centimeters and a radius of five centimeters. If there is only four centimeters of salsa left in the jar, then determine how much salsa is missing from the jar.

Answer 1

471.2 cm^3

Explanation:

We know that the salsa jars have a height of 10 cm and a radius of five cm.

So its volume is = base × height

Since, its base is circular so we can find the volume of the jar.

Volume of jar =
`\pi r^2h = 3.14 * 5^2 * 10` = 785.4 cm^3

Volume of salsa left in jar =
`\pi r^2h = 3.14 * 5^2 * 4` = 314.2 cm^3

Salsa missing from the jar = 785.4 - 314.2 = 471.2 cm^3

Answer 2

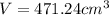`V=471.24cm^(3)` (simplified)

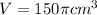`V=150\pi cm^(3)` (in terms of pi)

Explanation:

Since the salsa jar is basically a cylinder, to solve this we are using the formula for the volume of a cylinder:

`V=\pi r^(2) h`

where

`V` Is the volume of the cylinder (salsa jar)

`r` is the radius of the cylinder (salsa jar)

`h` is the height of the cylinder (salsa jar)

We know from our problem that height of the full salsa jar is 10 centimeters; we also know that that there are only 4 centimeters of salsa left in the salsa jar. So, to find the the height of the missing salsa, we just need to subtract the height of the salsa from the height of the full salsa jar:
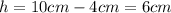`h=10cm-4cm=6cm`. Since the radius of the salsa jar never changes,
`r=5cm`.

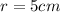Now we can replace the values in our volume formula to find how much salsa is missing from the jar:

`V=\pi r^(2) h`

`V=\pi (5cm)^(2) (6cm)`

`V=\pi (25cm^(2))(6cm)`

`V=150\pi cm^(3)`

`V=471.24cm^(3)`

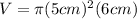
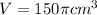
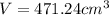
We can conclude that there are 471.24 cubic centimeters missing from the jar, or in terms of pi:
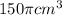`150\pi cm^(3)`.