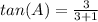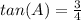Question

PLEASE!! Question is attached!

Answer 1

Option C.
`tan(A)=(3)/(4)`

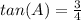
Explanation:

we know that

The tangent of angle A is equal to divide the opposite side to angle A (side BC) by the adjacent side to angle A ( side AB)

so

`tan(A)=(BC)/(AB)`

substitute the values

`tan(A)=(x)/(x+1)`

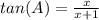
Applying the Pythagoras Theorem find the value of x

`(x+2)^(2)=x^(2)+(x+1)^(2)\\ \\x^(2)+4x+4=x^(2)+x^(2)+2x+1\\ \\x^(2) -2x-3=0`

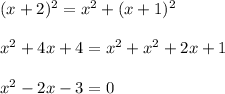
using a graphing calculator-----> solve the quadratic equation

The solution is x=3 -----> see the attached figure

substitute the value of x in the tan(A)

`tan(A)=(3)/(3+1)`

`tan(A)=(3)/(4)`