Question

What is the equation of the line shown?

Answer 1

2x-y-3=0

Explanation:

Here the line crosses the y -axis at −3 , so the y -intercept is −3 .

Here the line crosses the x -axis at 1.5 , so the x -intercept is 1.5 .

If x=0, then y= -3 because

-y-3=0

-y=3

y= -3

If y=0, then x=1.5 because

2x-3=0

2x=3

x=1.5

Answer 2

Hello!

The answer is:

The third option,

`2x-y-3=0`

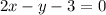
Why?

From the graphic we know that we are looking for a function that cut the x-axis at 2.5 and the y-axis at -3, also, the function has an increasing slope.

So, which function can meet all the mentioned before?

Let's try with each given equation and discard:

- First function:

`x-2y-3=0`

`y=(x-3)/(2)`

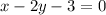
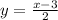
Finding the x-axis intercept by making y equal to 0, we have:

`x-2y-3=0\\\\2y=x-3\\\\[tex]y=(x-3)/(2)\\\\0=(x-3)/(2)\\\\(2)*(0)=x-3\\\\x-3=0\\\\x=3`

Now, making "x" equal to 0, to find the y-axis intercept, we have:

`y=(x-3)/(2)\\\\y=(0-3)/(2)=(-3)/(2)`

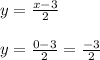
So, for the first function we have that it has a positive slope and the intercepts with the x-axis(3,0) and the y-axis (0,-1.5), hence, this function does not match with the given graph.

- Second function:

`2x-y+3=0`

`2x+3=y`

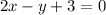
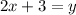
Finding the x-axis intercept by making y equal to 0, we have:

`2x+3=y\\\\2x+3=0\\\\2x=-3\\\\x=(-3)/(2)=-1.5`

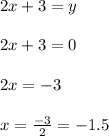
Now, making "x" equal to 0, to find the y-axis intercept, we have:

`2x+3=y\\\\2*(0)+3=y\\\\y=3`

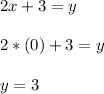
So, for the second function we have that it has a negative slope and the intercepts with the x-axis(-1.5,0) and the y-axis (0,3), hence, this function does not match with the given graph.

- Third function:

`2x-y-3=0`

`2x-3=y`

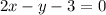
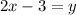
Finding the x-axis intercept by making y equal to 0, we have:

`2x-3=y\\\\2x-3=0\\\\2x=3\\\\x=(3)/(2)=1.5`

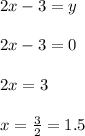
Now, making "x" equal to 0, to find the y-axis intercept, we have:

`2x-3=y`

`2*(0)-3=y`

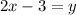
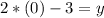
So, for the third function we have that it has a positive slope and the intercepts with the x-axis(1.5,0) and the y-axis (0,-3), hence, this function matchs with the given graph.

Hence, the answer is:

The third option,

`2x-y-3=0`

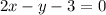
Have a nice day!