Hello!
The answer is:
The third option,

Why?
From the graphic we know that we are looking for a function that cut the x-axis at 2.5 and the y-axis at -3, also, the function has an increasing slope.
So, which function can meet all the mentioned before?
Let's try with each given equation and discard:
- First function:
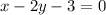
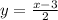
Finding the x-axis intercept by making y equal to 0, we have:
![x-2y-3=0\\\\2y=x-3\\\\[tex]y=(x-3)/(2)\\\\0=(x-3)/(2)\\\\(2)*(0)=x-3\\\\x-3=0\\\\x=3](https://img.qammunity.org/2020/formulas/mathematics/middle-school/sk3y9f8fzjuv6gf8cidu6dy9h0wu95w8rz.png)
Now, making "x" equal to 0, to find the y-axis intercept, we have:
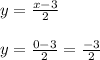
So, for the first function we have that it has a positive slope and the intercepts with the x-axis(3,0) and the y-axis (0,-1.5), hence, this function does not match with the given graph.
- Second function:

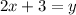
Finding the x-axis intercept by making y equal to 0, we have:
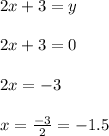
Now, making "x" equal to 0, to find the y-axis intercept, we have:
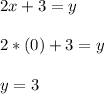
So, for the second function we have that it has a negative slope and the intercepts with the x-axis(-1.5,0) and the y-axis (0,3), hence, this function does not match with the given graph.
- Third function:

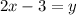
Finding the x-axis intercept by making y equal to 0, we have:
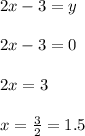
Now, making "x" equal to 0, to find the y-axis intercept, we have:
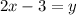
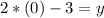
So, for the third function we have that it has a positive slope and the intercepts with the x-axis(1.5,0) and the y-axis (0,-3), hence, this function matchs with the given graph.
Hence, the answer is:
The third option,

Have a nice day!