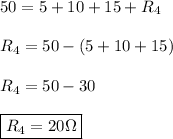Answer:
Explanation:
If resistors are in series, so the current
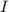 is the same in all of them. In this problem we have four resistors. So, we can get a relationship between the Equivalent resistance of series combination and the four resistors as follows:
is the same in all of them. In this problem we have four resistors. So, we can get a relationship between the Equivalent resistance of series combination and the four resistors as follows:
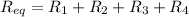
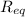 is the total resistance
is the total resistance
 . Moreover:
. Moreover:
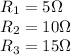
Therefore: