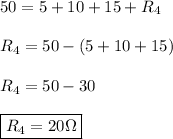Question

Four resistors are connected in series such that their total resistance is 50ohm . If the resistance of resistors is 5 ohm , 10ohm and 15 ohm respectively .find tue resistance of the fourth resistor

Answer 1

`\boxed{R_(4)=20\Omega}`

Explanation:

If resistors are in series, so the current
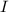`I` is the same in all of them. In this problem we have four resistors. So, we can get a relationship between the Equivalent resistance of series combination and the four resistors as follows:

`R_(eq)=R_(1)+R_(2)+R_(3)+R_(4)`

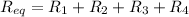
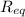`R_(eq)` is the total resistance
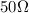`50\Omega`. Moreover:

`R_(1)=5\Omega \\ R_(2)=10\Omega \\ R_(3)=15\Omega`

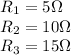
Therefore:

`50=5+10+15+R_(4) \\ \\ R_(4)=50-(5+10+15) \\ \\ R_(4)=50-30 \\ \\ \boxed{R_(4)=20\Omega}`