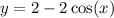ANSWER
The particular solution is:
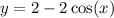
Step-by-step explanation
The given Ordinary Differential Equation is
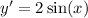
The general solution to this Differential equation is:
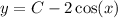
To find the particular solution, we need to apply the initial conditions (ICs)
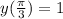
This implies that;
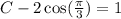
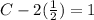
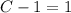
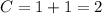
Hence the particular solution is